When an array element is in the ith row and jth column is called the element i, jo (i, j)-ith the array. Put back first rows and then columns.

Briefly usually expressed as A = (aij) with i = 1, 2, ..., m, j = 1, 2, ..., n. The subscripts indicate the element's position within the array, the first denotes the row (i) and the second column (j). For example the element a25 is the element in row 2 and column 5.
TO resolve these matrices,there are some methods to do :
Gauss-Jordan Reduction
Elementary row operations are:
1. Replace Ri by ari where a is a nonzero number (in words: multiply or divide a row by a nonzero number).
2. Replace Ri by ari ± BRJ where a is a nonzero number (replacing a row by a linear combination with another line).
3. Swap two rows
By using these three operations, we can set any matrix in reduced form. A matrix is reduced, or reduced row echelon form if:
P1. The first nonzero element in each row (called the highlight of that line) is 1.
P2. The columns of the highlights are cleared (ie, contain zero in every position above and below the central element.) The process of clearing a column by use of row operations is called swinging.
P3. The important element in each row is on the right of the highlight of the previous row and the rows of zero (if any) are at the bottom of the array.
The procedure to reduce a matrix to reduced echelon form is also called Gauss-Jordan reduction.
ELIMINACION GAUSSIANA
The Gaussian elimination method for solving systems of linear equations is to make basic operations through calls row operations into an equivalent system whose response easier to read directly. The Gaussian elimination method is the same for systems of equations 2 × 2, 3 × 3, 4 × 4 and so long as they respect the relationship of at least one equation for each variable.
Before illustrating the method with an example, we must first know the basic operations of line which are presented below:
1. Both members of an equation can be multiplied by a constant different from zero.
2. Nonzero multiples of an equation can join another equation
3. The order of the equations is interchangeable.
Once the operations known in my quest to solve
LU factorization
In linear algebra, factorization or decomposition LU (Lower-Upper English) is a form of a matrix factorization as the product of a lower triangular matrix and an upper. Due to instability of this method, for example if an element of the diagonal is zero, it is necessary premultiply matrix by a permutation matrix. Method called factorization PA = LU LU pivot.
This decomposition is used in numerical analysis to solve systems of equations (more efficiently) or find the inverse matrices.
matrcise lu
Cramer method (for determining)
It applies if the system has as many equations as unknowns n = m and the determinant of the coefficient matrix is nonzero. That is, a Cramer system is, by definition, compatible determined and, therefore, always has a unique solution.
The unknown value of each xi is obtained from a ratio whose denominator is the determinate of the coefficient matrix, whose numerator is the determinant obtained by changing the column i of the determinant above the column of independent terms.
EXAMPLE:
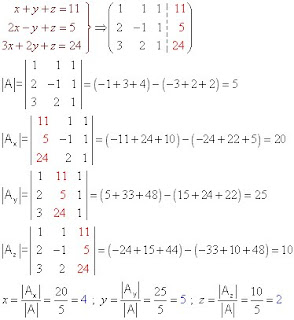
No hay comentarios:
Publicar un comentario